西门子一级-驱动器总代理商
更新:2025-11-08 08:18 编号:19658642 发布IP:116.224.103.5 浏览:4次



- 发布企业
- 上海兆维智控科技有限公司
- 认证
- 资质核验:已通过营业执照认证入驻顺企:第1年主体名称:上海兆维智控科技有限公司组织机构代码:91310120MAEBD1A69W
- 报价
- 请来电询价
- 品牌
- 西门子
- 型号
- 模块
- 产地
- 德国
- 关键词
- PLC,CPU,触摸屏,变频器,交换机,电机,电线,电缆,低压,
- 所在地
- 上海市奉贤区环城西路3111弄300号2幢1层
- 联系电话
- 15618725685
- 全国服务热线
- 15618725685
- 经理
- 岳经理 请说明来自顺企网,优惠更多
- 请卖家联系我
 15618725685
15618725685- 3998188751
详细介绍
电路分析中把电路与电源的接通、切断,电路参数的突然改变,电路联接方式的突然改变,电压源的电压或电流源的电流的突然改变等,统称为换路(switching),且认为换路是即刻完成的。 在§1和§2中曾经指出:线性电容元件上的电压(或电荷量)的变化直接受到电容电流的约束、有限电容电流规定了电容电压(或电荷量)的连续变化;电容电压(或电荷量)的跳变则必然伴有无限大的电容电流。线性电感元件中的电流(或磁通链)的变化直接受到电感电压的约束,有限电感电压规定了电感电流(或磁通链)的连续变化;电感电流(或磁通链)的跳变则必然伴有无限大的电感电压。 在电路分析中,一般以换路发生的时刻作为计算时间的起点,即认为换路是在t=0时发生的。为了用数学式来表达在换路前后的转折瞬间,在有限电容电流的条件下电容元件上的电荷(或电压)不能跳变的规律,以及在有限电感电压的条件下电感元件中的磁通链(或电流)不能跳变的规律,我们规定 磁通链 我们把动态电路中各独立电容电压(或电荷量)和各独立电感电流(或磁通链)在 电路的初始状态,在一般情况下,可以根据电路的原始状态应用式(1)至式(4)求出。至于电路中其它电压、电流的初始值(例如电阻中的电压和电流、电感电压、电容电流等变量的初始值),可根据换路后的电路和电容电压、电感电流的初始值,以及独立源在 |
含有动态元件(即储能元件)的电路称为动态电路(dynamic circuit)。由于动态元件的电压与电流之间呈导数关系或积分关系,根据基尔霍夫定律对动态电路列出的方程是微分方程或积分微分方程。以图1所示电路为例,根据基尔霍夫电压定律可得
![]() (1)
(1)
假设电路的待求变量是![]() ,把电容元件的电压
,把电容元件的电压
电流关系 ![]() 图 1 简单动态电路
图 1 简单动态电路
代入式 (1)经整理后得到
![]() (2)
(2)
在电路分析中,作为输入激励的电压或电流可简称输入(input),而作为待求响应(或变量)的电压或电流可简称输出(output)。
只含有一个激励源和一个输出变量的电路称为单输入—单输出电路(singal-input singal-output circuit)。式(2)是联系图1所示电路的输人![]() 与输出
与输出![]() 之间关系的单一变量微分方程,称为该电路的输人—输出方程。对于线性电路,输人—输出方程是常系数线性微分方程。
之间关系的单一变量微分方程,称为该电路的输人—输出方程。对于线性电路,输人—输出方程是常系数线性微分方程。
对于图1所示的电路,当求出![]() 后,可应用元件的电压电流关系式
后,可应用元件的电压电流关系式 ![]()
![]()
![]()
求出电路中的电流和任一元件的电压。
可以证明有几个动态元件,其动态电路的输入输出方程就有几阶
对于任何一个已知的单输入—单输出的动态电路,应用基尔霍夫定律与电路 中各元件的电压电流关系,总可以求出其输人—输出方程。电路越复杂,获得此方程所需要的工作量就越大。下面以图2所示电路为例说明复杂电路输入—输出方程的建立及输入—输出方程的一般形式。
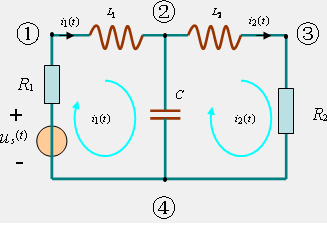
图 2 多回路的动态元件
图2是含有三个动态原件两个网孔四个节点的动态电路,应用§2—6的回路分析法可建立两个独立回路方程
![]() (3a)
(3a)
![]() (3b)
(3b)
由式(3)可知,对动态电路建立的回路方程是一组联立的积分微分方程。类似地,若对图2所示电路应用§2—7的节点分析法建立节点方程,则所得节点方程也是一组联立的积分微分方程。
现在假设电路的输出变量是回路电流![]() ,从回路方程式(3)来推求图2所示单输入—单输出电路的输入—输出方程。
,从回路方程式(3)来推求图2所示单输入—单输出电路的输入—输出方程。
将式(3a)与式(3b)相加,得
![]() (4)
(4)
将式 (3a)对t 求导,得
![]()
由此式可得 ![]() (5)
(5)
将式 (5)对t 求导,得
![]() (6)
(6)
将式(5)与式(6)代入式(4),经移项整理后,得到
 (7)
(7)
式(7)就是图2所示电路以![]() 作为输出变量的输入—输出方程。这是一个三阶的常系数线性微分方程,其中
作为输出变量的输入—输出方程。这是一个三阶的常系数线性微分方程,其中![]() 和
和![]() 的系数及其各阶导数的系数都是常数。以回路电流
的系数及其各阶导数的系数都是常数。以回路电流![]() 作为输出变量,亦可得到类似的输入—输出方程。
作为输出变量,亦可得到类似的输入—输出方程。
由以上分析可以看出:对一般动态电路建立的电路方程是一组联立的微分方程,或一组联立的积分微分方程[见式(4—4—3)]。由此联立方程组出发,总可以求出对应于电路中任一输出变量的输入—输出方程。在一般情况下,这是一个高阶的常系数线性微分方程。电路越复杂,所含动态元件越多,方程的阶数就越高。
根据前面的分析,可以写出描述单输入—单输出动态电路的输入—输出程的一般形式为
 (8)
(8)
式中r(t)表示电路的输出,f(t)表示作为输人的电压源的电压或电流源的电流的时间函数式。
我们可以说,对单输入—单输出动态电路的分析可以归结为建立以待求变量作为输出变量的输入—输出方程和求解这一方程。
一般地说,如果描述动态电路的输人—输出方程是一阶微分方程,则称该电路为一阶电路。如果输入—输出方程是n阶微分方程,则相应的电路称为n阶电路。据此,图1所示电路为二阶电路,图2所示电路为三阶电路。
- 我们的产品目录
- 西门子S7-1500CPU
- 西门子S7-1200精智面板
- 西门子S7-1200精简面板
- 西门子S7-1200存储卡
- 西门子S7-1200单相电源模块
- 西门子S7-1200故障安全继电器输出
- 西门子S7-1200故障安全量数字模块
- 西门子S7-1200通用连接电缆
- 西门子S7-1200信号板扩展模块
- 西门子S7-1200通信处理器/模块
- 西门子S7-1200模拟量扩展模块
- 西门子S7-1200数字量扩展模块
- 西门子S7-1200CPU
- LOGO!逻辑模块
- LOGO!控制器
- S7-400-CPU模块中央处理器
- 西门子S7-1500电源
- S7-200模拟IO
- S7-200数字IO模块
- S7-200紧凑型CPU
- S7-200扩展模拟模块
- S7-200扩展数字模块
- 西门子S7-200
- 西门子S7-300
- 触摸屏
- 200CN
- S120
- 西门子S7-1500
- 西门子
- 西门子6GK交换机
| 成立日期 | 2025年02月21日 | ||
| 法定代表人 | 汤忠伟 | ||
| 注册资本 | 218 | ||
| 主营产品 | 我们是西门子工控产品专业服务提供商,欢迎来电来函咨询,合作共赢,共同发展! | ||
| 经营范围 | 一般项目:技术服务、技术开发、技术咨询、技术交流、技术转让、技术推广;软件开发;电子元器件与机电组件设备销售;电子元器件批发;工业自动控制系统装置销售;电气设备销售;电气设备修理;仪器仪表销售;仪器仪表修理;工业机器人安装、维修;工业机器人销售;专用设备修理;计算机及通讯设备租赁;机械设备租赁;电子产品销售;五金产品零售;金属材料销售;办公设备耗材销售;互联网销售(除销售需要许可的商品);日用品销售;办公用品销售;人工智能应用软件开发;人工智能基础软件开发;人工智能硬件销售;人工智能行业应用系统集成服务;人工智能公共数据平台;信息系统集成服务;人工智能双创服务平台;网络技术服务;计算机系统服务;电子、机械设备维护(不含特种设备);普通机械设备安装服务;会议及展览服务;市场营销策划;体验式拓展活动及策划;知识产权服务(专利代理服务除外);版权代理;科技中介服务;租赁服务(不含许可类租赁服务);税务服务;计算机软硬件及辅助设备零售;通用设备修理。(除依法须经批准的项目外,凭营业执照依法自主开展经营活动) | ||
| 公司简介 | SIEMENS可编程控制器1、SIMATICS7系列PLC:S7-200、S7-1200、S7-300、S7-400、ET-2002、逻辑控制模块LOGO!230RC、230RCO、230RCL、24RC、24RCL等3、SITOP直流电源24VDC1.3A、2.5A、3A、5A、10A、20A、40A可并联.4、HMI触摸屏TD200TD400CK-TPOP177TP177,MP277MP377 ... | ||
- 西门子工控机环境温湿度监控实用技术解析西门子工控机环境温湿度监控实用技术解析随着工业自动化的不断深入,工控机作为核心硬... 2025-07-17
- 西门子工控机多任务处理能力提升方案西门子工控机多任务处理能力提升方案西门子工控机在工业自动化领域广泛应用,其多任务... 2025-07-17
- 西门子工控机数据传输速率提升方法说明西门子工控机数据传输速率提升方法说明随着工业自动化程度的不断提高,西门子工控机在... 2025-07-17
- 西门子工控机存储设备故障修复技巧详解西门子工控机存储设备故障修复技巧详解西门子工控机以其高稳定性和可靠性广泛应用于工... 2025-07-17
- 西门子工控机性能优化调试全流程分享西门子工控机性能优化调试全流程分享随着工业自动化的不断升级,西门子工控机作为核心... 2025-07-17
 西门子电线电缆-驱动器总代理品牌:西门子
西门子电线电缆-驱动器总代理品牌:西门子 西门子变频器-驱动器总代理品牌:西门子
西门子变频器-驱动器总代理品牌:西门子 西门子plc模块-驱动器总代理品牌:西门子
西门子plc模块-驱动器总代理品牌:西门子 西门子cpu模块-驱动器总代理品牌:西门子
西门子cpu模块-驱动器总代理品牌:西门子 西门子一级-驱动器总代理品牌:西门子
西门子一级-驱动器总代理品牌:西门子 西门子授权-驱动器总代理商品牌:西门子
西门子授权-驱动器总代理商品牌:西门子 西门子模块-驱动器总代理商品牌:西门子
西门子模块-驱动器总代理商品牌:西门子 西门子cpu模块-驱动器总代理商品牌:西门子
西门子cpu模块-驱动器总代理商品牌:西门子 西门子plc模块-驱动器总代理商品牌:西门子
西门子plc模块-驱动器总代理商品牌:西门子 西门子变频器-驱动器总代理商品牌:西门子
西门子变频器-驱动器总代理商品牌:西门子









