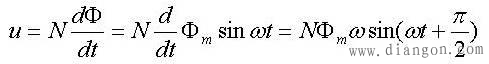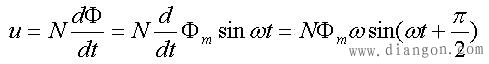西门子数控系统|驱动器总代理商|2023
更新:2023-10-26 04:00 编号:19464625 发布IP:116.224.103.5 浏览:2次





- 发布企业
- 浔之漫智控技术(上海)有限公司商铺
- 认证
- 资质核验:已通过营业执照认证入驻顺企:第3年主体名称:浔之漫智控技术(上海)有限公司组织机构代码:91310117MA1J3R698D
- 报价
- 请来电询价
- 品牌
- 西门子
- 型号
- 模块
- 产地
- 德国
- 关键词
- PLC,CPU,触摸屏,变频器,交换机,电机,电线,电缆,低压,
- 所在地
- 上海市松江区广富林路4855弄88号3楼
- 联系电话
- 15821971992
- 全国服务热线
- 15821971992
- 经理
- 聂聪 请说明来自顺企网,优惠更多
详细介绍
当电压为正弦波时,磁通也为正弦波,但电流却是具有尖顶的非正弦波,这种波形畸变是由于磁饱和所造成的。电压越高,磁通越大,铁芯饱和越严重,则电流波形畸变后变得更尖。若电压与磁通的振幅都较小,铁芯没有饱和,则电流波形将更接近正弦波。当电流作正弦变化且工作至饱和区域时,磁通具有平顶波形,如图所示。
|
交流铁芯线圈如图所示,线圈两端加一交流电压,则线圈中的电流将产生磁通,方向符合右手螺旋法则。
设电压为正弦量时,磁通也是正弦量,即: 根据电磁感应定律,得:
由此式可看出电压的相位比磁通超前90°,并得感应电压的有效值与主磁通的*大值的关系为
注意: 由此可知当电源频率和线圈匝数一定时,交流铁芯线圈磁通的*大值与线圈外加电压的有效值成正比,与铁芯的材料和尺寸无关。 |
对称分支磁路就是磁路存在着对称轴,轴两侧磁路的几何形状完全对称,相应部分的材料也相同,两侧作用的磁通势也是对称的,如图8-15所示的轴。
根据磁路定律,这种磁路的磁通分布也是对称的。当已知对称分支磁路的磁通求磁通势时,只要取对称轴的一侧磁路计算即可求出整个磁路所需的磁通势。取对称轴一侧磁路计算时,中间铁芯柱(对称轴)的面积为原铁芯柱的一半,中间柱(对称轴)的磁通也减为原来的一半。但磁感应强度和磁通势却保持不变。这种磁路的计算也有两类问题:一类是已知磁通求磁通势;另一类是已知磁通势求磁通。具体的计算步骤及方法同无分支磁路。 |
已知磁通求磁通势无分支磁路的主要特点是磁路有相等的磁通,如已知磁通和各磁路段的材料及尺寸,可按下述步骤去求磁通势:
例题8-1: 图8-13(a)所示磁路,图上标明尺寸单位为,铁芯所用硅钢片上的基本磁化曲线如图8-13(b),填充因数,线圈匝数为120,试求在该磁路中获得磁通所需的电流? 解: (1)该磁路由硅钢片和空气隙构成,硅钢片有两种截面积,该磁路分为三段来计算。 (2)求每段磁路的平均长度和截面积
(3)求每段磁路的感应强度
(4)求每段磁路的磁场强度:图8-13(b)所示曲线查得
(5)求每段磁路的磁压降
(6)求总磁通势
已知磁通势求磁通由于磁路的非线性缘故,对于已知磁通势求磁通的问题,不能根据上面的计算倒推过去。对这类问题一般采用试探法。 试探法:要先假定一个磁通,按已知磁通求磁通势的步骤,求出磁通的磁压降的总和,再和给定磁通势比较。如果与给定磁通势偏差较大,则修正假定磁通,再重新计算,直到与给定磁通势相近时,便可认为这一磁通就是所求值。 例题8-2 如图8-14所示磁路,中心线长度,磁路横截面面积是,气隙长度,线圈匝数1650匝,电流为时。铁芯为铸钢材料,基本磁化曲线可查附录一,试求磁路中的磁通? 解: 此磁路由铁芯段和气隙段组成。 铁芯段的平均长度和面积为:
气隙段的平均长度和面积为:
磁路中的磁通势为
磁通为
查附录一,得
空气隙的磁场强度
磁通势为
经过过几次试探,试探结果如表8-3所示。 从表8-3中,可看出第4次试探值作为*后结果,即所求磁通为
|
| 成立日期 | 2019年09月10日 | ||
| 法定代表人 | 袁宜男 | ||
| 注册资本 | 5000000 | ||
| 主营产品 | 西门子PLC模块、CPU模块、DP通讯电缆、6GK交换机、低压电器授权总代理商、代理商中国授权一级总代理商 | ||
| 经营范围 | 从事智能科技、自动化科技、机电领域内的技术开发、技术转让、技术咨询、技术服务,工业自动化设备安装,工业自动化控制设备、电气设备、机电设备、电子产品、五金产品、金属材料、仪器仪表、橡塑制品销售,商务信息咨询,软件开发,建筑装修装饰建设工程专业施工,建筑安装工程(除特种设备),机械设备租赁(不得从事金融租赁),物业管理。工业自动化设备加工、销售。【依法须经批准的项目,经相关部门批准后方可开展经营活动】 | ||
| 公司简介 | 浔之漫智控技术(上海)有限公司是中国西门子的合作伙伴,公司主要从事工业自动化产品的集成,销售和维修,是全国知名的自动化设备公司之一。公司坐落于中国一线城市上海市,我们真诚的希望在器件的销售和工程项目承接、系统开发上能和贵司开展多方面合作。以下是我司主要代理西门子产品,欢迎您来电来函咨询,我们将为您提供优惠的价格及快捷细致的服务!西门子华东区域代理SIEMENS可编程控制器1、SIMATICS7系列 ... | ||
- 西门子6ES7231-0HF22-0XA0详细使用3UG4621/3UG4622监控继电器3UG4621或3UG4622电流监控继... 2023-10-26
- 西门子6ES7231-0HC22-0XA8详细使用SIRIUS3UG4622监控继电器继电器监控单相AC电流(rms值)和DC电流... 2023-10-26
- 西门子6ES7223-1PM22-0XA8详细使用1、刀具的选择应满足:安装调整方便、刚性好、精度高、耐用度高等要求。1)刀具主要... 2023-10-26
- 西门子6ES7223-1BM22-0XA8详细使用根据被加工零件图纸,按照已经确定的加工路线和允许的编程误差,计算数控编程所需要的... 2023-10-26
- 西门子6ES7223-1PL22-0XA8详细使用1)G00、G01、G02、G03快速点定位G00X(U)_Z(W)_;直线插补... 2023-10-26
 西门子数控系统|低压电器总代理商|2023品牌:西门子
西门子数控系统|低压电器总代理商|2023品牌:西门子 西门子数控系统|低压总代理商|2023品牌:西门子
西门子数控系统|低压总代理商|2023品牌:西门子 西门子数控系统|plc模块总代理商|2023品牌:西门子
西门子数控系统|plc模块总代理商|2023品牌:西门子 西门子数控系统|cpu模块总代理商|2023品牌:西门子
西门子数控系统|cpu模块总代理商|2023品牌:西门子 西门子数控系统|一级总代理商|2023品牌:西门子
西门子数控系统|一级总代理商|2023品牌:西门子 西门子数控系统-一级代理商-2023品牌:西门子
西门子数控系统-一级代理商-2023品牌:西门子 西门子数控系统-cpu模块代理商-2023品牌:西门子
西门子数控系统-cpu模块代理商-2023品牌:西门子 西门子数控系统-plc模块代理商-2023品牌:西门子
西门子数控系统-plc模块代理商-2023品牌:西门子 西门子数控系统-低压代理商-2023品牌:西门子
西门子数控系统-低压代理商-2023品牌:西门子 西门子数控系统-低压电器代理商-2023品牌:西门子
西门子数控系统-低压电器代理商-2023品牌:西门子